熱傳導方程不僅揭示了鍛件在時間上非穩態性和空間上非均勻性之間的內在聯系，而且能對鍛件溫度場進行普遍描述。然而對熱傳導方程通解的求取，必須先要明確熱傳導方程的單值性條件，才能進一步確定一個特定的溫度場。鍛造過程中的單值性條件有：初始條件和邊界條件。

(1)初始條件

熱態鍛件在未受鍛造加工時，不受內部熱能影響。并受外界環境的影響時間也是極短，因此，在初始時刻 t=0，鍛件的溫度仍保持均勻分布。通過精密的測溫系統

求得鍛件初始溫度，即初始條件：

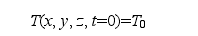
其中：T(x,y,z,t)為鍛件溫度場；T0為鍛件初始溫度場。

(2)邊界條件

熱傳導的過程中常用的邊界條件可以分為三類：狄利科利條件、紐曼條件、Robin條件。對于三類邊界的具體表述如下：

狄利科利條件是確定特定邊界 M 上的溫度和溫度隨時間變化規律，其表達式為：

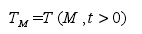
其中：TM為邊界上的溫度。

紐曼條件是確定了特定邊界M 上的熱流密度和溫度隨時間的變化規律。其表達式為：

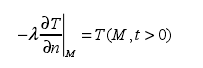
其中：n 為邊界 M 外法線方向。

Robin 條件是在確定了物體和外界換熱系數前提下，將物體邊界M處的溫度和其換熱數進行線性化的連接。其表達式為：

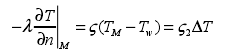
其中：TW為外界溫度。

在鍛造過程中，熱態鍛件主要受外界環境和鍛造加工作用的影響。由于鍛件尺寸變化，鍛件的形狀、表面積也在不斷地變化，并影響鍛件表面的熱交換系數。因此，結合鍛件的尺寸變化，需要對鍛件的表面熱傳導系數進行修正。本文以鍛壓過程中柱類鍛件為例進行研究，在相鄰單位時間內的熱流量是相差無幾的，即 Qτ ≈ Qτ+1。

因此，可得到如下關系式：

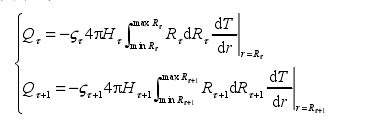
其中：?τ為在τ時刻下鍛件與其外界環境的交換熱傳導系數；max Rτ為在τ時刻下鍛件徑向測量尺寸的最大值；min Rτ 為在τ時刻下鍛件徑向測量尺寸的最小值；Hτ為τ時刻下的鍛件軸向測量尺寸。

結合上述的修正熱傳導系數，將 Robin 條件與鍛造過程測量的溫度、尺寸信息相結合，進而可確定鍛造過程中的熱傳導方程的邊界條件。在鍛造過程中，鍛件受外界環境影響作用時的徑向邊界條件為：

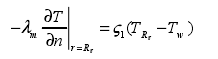
其中：λm為鍛件的導熱系數；Rτ為實時測量的鍛件徑向尺寸；?1 為受外界環境影響對流換熱系數；TRτ為鍛件徑向表面的溫度；Tw為環境溫度。可將方程式(2-7)與在特定時刻τ時鍛件測量溫度相結合，進一步進簡化為方程式(2-8)：

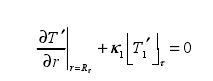
其中：T  ′為鍛件的溫度；?T'1τ為以外界環境為參考標準時的測量溫度；κ1為外界換環境下修正的熱交換系數和鍛件導熱系數的比值。由于在鍛造過程中鍛件的上下端面與鍛造砧子接觸，鍛造時接觸的換熱系數與以上在外界環境中的換熱系數是有所有所不同。因此，根據以上鍛件受外界環境影響作用時的邊界條件(2-7)的求取方法，可以獲得在鍛造過程中的鍛件上下端面邊界條件：

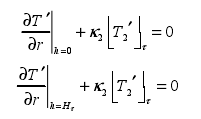
其中：?T'2?τ為鍛件端面的溫度；κ2為與砧子接觸時修正的熱交換系數與鍛件導熱系數的比值。

在熱態鍛件成形時，隨著鍛件幾何形狀和尺寸的不斷變化，使得鍛件與外部環境接觸的表面積也在不斷地變化。因此實時地結合鍛件的測量尺寸，通過修正熱交換系數的方法，將鍛件尺寸變化形狀因素對鍛件溫度的影響轉化為修正熱交換系數的方式對其進行補償，更加進一步體現了鍛件尺寸變化對鍛件溫度場研究重要意義。

鳳谷工業爐集設計研發,生產銷售,培訓指導,售后服務一體化,專利節能技術應用,每年為企業節省40%-70%的能源成本,主要產品加熱爐,工業爐,節能爐,蓄熱式爐,垃圾氣化處理設備，歡迎致電咨詢:0510-88818999